На плечах гигантов, на спинах электронов
Кубок Полесья-2001, Гомель 2001-05-05
Второй тур
Вопрос 8: Декан математического факультета Геттингена Клейн правил подчиненным, что называется, железной рукой. Приват-доцент Цермело решил насолить строгому администратору и обнародовал такую логическую задачку: "Все математики Геттингена принадлежат к двум классам. Одни делают то, что не нравится им, но нравится Клейну. Другие делают то, что нравится им, но не нравится Клейну. К какому классу относится в таком случае сам Клейн?" Решите и вы эту задачку, учтя, что "ни к какому" – ответ не для математиков...
Он принадлежит классу не-математиков.
Цермело хотел своей задачей сделать нелестный для Клейна вывод, что тот не является математиком.
Если бы Клейн был математиком, то он должен был бы принадлежать хотя бы одному классу, но он не не принадлежит никакому из них, след, по закону контрапозиции математиком не является
Один против дюжины. 2001 год 2001-01-01
Тур 39
Вопрос 13: Услышав одно из названий ЭТОГО, не слишком образованный человек мог бы предположить, что ЭТО имеет нечто общее с числами 13 или 22, хотя на самом деле название происходит от фамилии известного математика. Что же ЭТО?
Число Непера
Чемпионат Днепропетровска сезона 2002/03 гг. Высшая лига 2002-01-01
Команда "Flash"
Вопрос 15: Господа знатоки, закончите следующий анекдот. Жили два друга – математик и музыкант. Музыкант не раз предлагал математику сходить на какой-нибудь концерт, но тот всегда отказывался. Однажды музыкант сказал своему другу следующее: "Пойдем, будет выступать прекрасный (слово пропущено) оркестр", после чего математик сразу согласился. После концерта музыкант спросил у математика, понравился ли ему концерт, но тот разочарованно ответил: "Ничего интересного, ведь k равно...". Если вы поняли, какое слово было пропущено, то легко сможете ответить, чему равно k?
k=3
Вопрос 20:
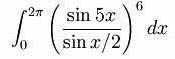
Перед вами формула, по которой можно вычислить точное количество ТАКИХ ИХ. В среднем же один ОН из восемнадцати является ТАКИМ. Герой одного из романов Переса-Реверте пытался продать коллекцию из 5775 ТАКИХ ИХ. Какой эпитет мы заменили словом "ТАКОЙ"?
"счастливый"
Вопросы Дмитрия Жаркова, клуб "Мозговорот", 1998 1998-01-01
Блок 7
Вопрос 21: Как-то раз у Эйнштейна спросили: почему Бог, создав мир логическим и сообразным, допустил, чтобы существовали неберущиеся интегралы – те, решение которых не представляется в виде формулы. Эйнштейн ответил, что Богу эта проблема незнакома. Почему?
Бог придумал берущиеся интегралы; всё остальное дело рук математиков.
Курск-2006 2006-01-07
5 тур
Вопрос 23:

На фотографии вы видите Дэйва Байера, математика-консультанта фильма "Игры разума", с системой уравнений, которую он придумал для одной из сцен фильма. Байер хотел, чтобы Нэш в фильме предложил студентам для раздумий имеющую реальный глубокий математический смысл, лаконичную и в чем-то парадоксальную задачу. Посмотрите на строки, выражающие ее, и ответьте, математическим ЧЕМ назвали ее в журнале "Science" после выхода фильма.
хайку (хокку)
Второй тур
Вопрос 8: Декан математического факультета Геттингена Клейн правил подчиненным, что называется, железной рукой. Приват-доцент Цермело решил насолить строгому администратору и обнародовал такую логическую задачку: "Все математики Геттингена принадлежат к двум классам. Одни делают то, что не нравится им, но нравится Клейну. Другие делают то, что нравится им, но не нравится Клейну. К какому классу относится в таком случае сам Клейн?" Решите и вы эту задачку, учтя, что "ни к какому" – ответ не для математиков...
Он принадлежит классу не-математиков.
Цермело хотел своей задачей сделать нелестный для Клейна вывод, что тот не является математиком.
Если бы Клейн был математиком, то он должен был бы принадлежать хотя бы одному классу, но он не не принадлежит никакому из них, след, по закону контрапозиции математиком не является
Один против дюжины. 2001 год 2001-01-01
Тур 39
Вопрос 13: Услышав одно из названий ЭТОГО, не слишком образованный человек мог бы предположить, что ЭТО имеет нечто общее с числами 13 или 22, хотя на самом деле название происходит от фамилии известного математика. Что же ЭТО?
Число Непера
Чемпионат Днепропетровска сезона 2002/03 гг. Высшая лига 2002-01-01
Команда "Flash"
Вопрос 15: Господа знатоки, закончите следующий анекдот. Жили два друга – математик и музыкант. Музыкант не раз предлагал математику сходить на какой-нибудь концерт, но тот всегда отказывался. Однажды музыкант сказал своему другу следующее: "Пойдем, будет выступать прекрасный (слово пропущено) оркестр", после чего математик сразу согласился. После концерта музыкант спросил у математика, понравился ли ему концерт, но тот разочарованно ответил: "Ничего интересного, ведь k равно...". Если вы поняли, какое слово было пропущено, то легко сможете ответить, чему равно k?
k=3
Вопрос 20:
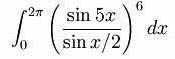
Перед вами формула, по которой можно вычислить точное количество ТАКИХ ИХ. В среднем же один ОН из восемнадцати является ТАКИМ. Герой одного из романов Переса-Реверте пытался продать коллекцию из 5775 ТАКИХ ИХ. Какой эпитет мы заменили словом "ТАКОЙ"?
"счастливый"
Вопросы Дмитрия Жаркова, клуб "Мозговорот", 1998 1998-01-01
Блок 7
Вопрос 21: Как-то раз у Эйнштейна спросили: почему Бог, создав мир логическим и сообразным, допустил, чтобы существовали неберущиеся интегралы – те, решение которых не представляется в виде формулы. Эйнштейн ответил, что Богу эта проблема незнакома. Почему?
Бог придумал берущиеся интегралы; всё остальное дело рук математиков.
Курск-2006 2006-01-07
5 тур
Вопрос 23:

На фотографии вы видите Дэйва Байера, математика-консультанта фильма "Игры разума", с системой уравнений, которую он придумал для одной из сцен фильма. Байер хотел, чтобы Нэш в фильме предложил студентам для раздумий имеющую реальный глубокий математический смысл, лаконичную и в чем-то парадоксальную задачу. Посмотрите на строки, выражающие ее, и ответьте, математическим ЧЕМ назвали ее в журнале "Science" после выхода фильма.
хайку (хокку)
-
-
18.10.2008 в 12:52-
-
18.10.2008 в 12:52изменения во времени клантового объекта???
мозг-нейроны-потенциалы-кванты
изменения во времени= динамика -игры
гальвани - биоэлектричество...
гамильтониан - постоянная планка - потенциал дейстия
-
-
18.10.2008 в 12:53два раз не и следовательно раскрыть
-
-
18.10.2008 в 12:55это был ответ не на этот коммент а на предыдущий)
вставила уже)))
-
-
18.10.2008 в 12:56"Бог придумал берущиеся интегралы; всё остальное дело рук
дьяволачеловека".-
-
18.10.2008 в 12:58-
-
18.10.2008 в 12:59-
-
18.10.2008 в 12:59Есть какой-то способ брать все интегралы?
-
-
18.10.2008 в 13:00дьяволачеловека" красиво)-
-
18.10.2008 в 13:00Лямбда права!!!
А??? Да ведь???
-
-
18.10.2008 в 13:02Если серьзно, то математики в эту фразу напрашиваются
-
-
18.10.2008 в 13:04Здорово!
Я думаю, так оно и есть!
(В смысле про фразу, а не про то, кто придумал неберущиеся интегралы))))
-
-
18.10.2008 в 13:04-
-
18.10.2008 в 13:05-
-
18.10.2008 в 13:06-
-
18.10.2008 в 13:06численные методы
-
-
18.10.2008 в 13:07а может Б-г использует численные методы, кстати? Раз они такие сильномогучие?
-
-
18.10.2008 в 13:08Ему не надо, Он знает и так)))
-
-
18.10.2008 в 13:11Бог придумал берущиеся интегралы; всё остальное дело рук математиков. (Лямбда)
Эйнштейн ответил, что Богу эта проблема незнакома. Почему?
Он использует численные методы (В.Д)
???
-
-
18.10.2008 в 13:13Нет, говорю же: Богу не нужны численные методы чтобы считать площади и объемы. Он их знает. Так же как знает любой определенный интеграл. А неопределенный неберущийся никому не нужен. И численными методами он тоже не решится.
-
-
18.10.2008 в 13:18— Есть какой-то способ брать все интегралы?
— численные методы
Я просто отталкивалась от предыдущей гипотезы Лямбды - для Б-га все интегралы берущиеся
Ну, не знаю
Я матан не люблю
-
-
18.10.2008 в 13:19а я не люблю численные методы (((
А если учесть, что это был профиль нашей кафедры (выч.мат) то проходили мы их со второго по пятый курс.
Нет, это не Богово дело ))))))
-
-
18.10.2008 в 13:20-
-
18.10.2008 в 13:22я в интегралах полный синус(
-
-
18.10.2008 в 13:22нельзя так говорить (((
пойду я наверное Перес-Реверте почитаю. Потому что явно сама по себе формула тут ни при чем.
Должно быть что-то легкое.
А насчет 23 — Триумф вполне может быть верно!
Надо еще подумать...
-
-
18.10.2008 в 13:26-
-
18.10.2008 в 13:26-
-
18.10.2008 в 13:27и числовые методы=))))))
-
-
18.10.2008 в 13:29-
-
18.10.2008 в 13:34Вроде как дано пространство чего-то (или группа), потом подпространство (или подгруппа)
И надо найти размерность
не тянет это на триумф
P.S
А V, W стандартные обозначения для пространств.